The smart-Kd concept
Joint research projects: ESTRAL – WEIMAR – SMILE
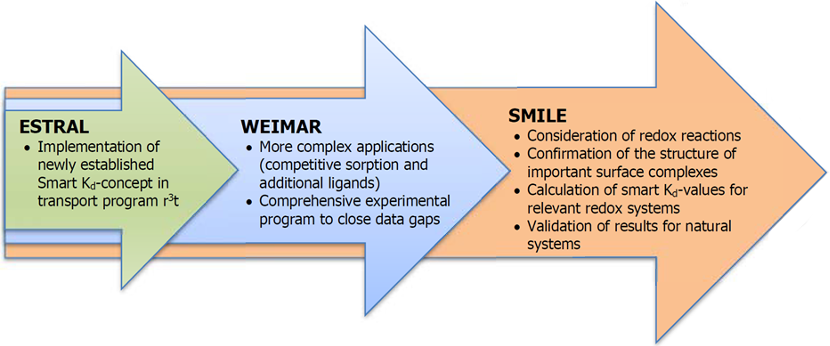
In 2008, a series of three subsequent research projects was initiated with the aim to develop a concept to describe sorption in transport models for performance assessment (PA) codes of deep geological repositories as a transient process since environmental conditions are changing with time. Consequently, geochemical parameters for long-term safety relevant elements vary temporally and/or spatially. This can lead to significant changes in the sorption behavior of radionuclides. Originally developed in ESTRAL, the concept was then extended to more complex geochemical conditions in the following project WEIMAR and is now being further improved and tested in the most recent project SMILE:
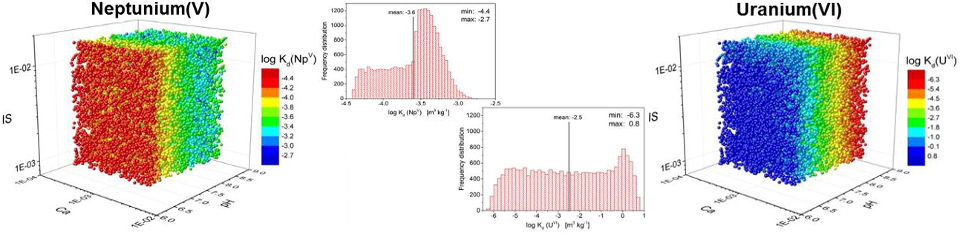
Data from both research projects, together with published results now form a more comprehensive and reliable database for the application of the smart Kd‑concept. This new concept is mainly based on surface complexation modeling and ion exchange. It applies the component additivity approach for competitive mineral-specific sorption to calculate realistic distribution coefficients for natural sediment and rock systems over a wide range of environmental parameters (e.g. pH, ionic strength, concentration of dissolved inorganic carbon and calcium). This new methodology has various benefits:
- rapid computation of Kd‑values for large numbers of environmental parameter combinations, including ones with experimentally difficult-to-access conditions,
- impact of spatial and temporal variable geochemistry is considered in PA models,
- efficiency in computing time is ensured for long time scales and large areas, and
- uncertainty and sensitivity analyses are also provided.
We offer topics for Bachelor and Master theses, please feel free to contact us.